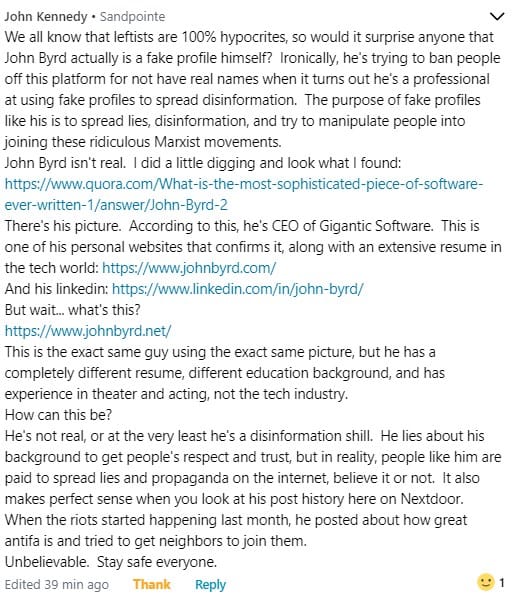
Bluegrass. It’s a totally American music. Born around the same time as rock and roll, it developed in a parallel path, touching other musics and being touched by them.
I’m choosing bluegrass for you because it is what I remember. It was an old music already, when I was growing up in Sissonville, West Virginia. It always seemed to be back in the corner of consciousness — the only thing the radio would receive, on those long car trips to the trailer at Franklin.
Like all musics, we have to choose a starting place for bluegrass, and if we were to be fair, we’d have to go back through bluegrass’s Scotch-Irish roots, to the country dances of the Old World and to the rich ballad tradition there. And we’d have to include work songs and the banjo as an instrument of purely African heritage.
But I’m going to lie to you, and say that bluegrass started in Dallas of 1927, and we’ll listen to a recording that Blind Lemon Jefferson had to travel all the way to Chicago to lay down:
A sparse recording of a modified blues progression. Not much there, really, until you notice the fingerpicking and the blues singing that turned into several different kinds of American musics in the decades to come.
Let’s move to Bristol, Tennessee. It’s 1927. That guitar is being picked on by one Maybelle Carter:
Yet again, that fingerpicking, with the melody in the bass line. Totally unlike the Dixieland frailing sound that you get when you strum the guitar. Here and as above, the guitar serves as its own rhythm instrument. This is a novel sound, and it’s transmitted out of Maces Spring, Virginia, and Ceredo, West Virginia, and anyplace else big enough to set up an antenna and a phonograph player.
Bluegrass and radio are deeply intermixed. In the Appalachian hills, the presence of one meant the presence of the other. My grandfather did tap dancing shows on a local radio station when he was young. The shows always featured local talent playing local songs, and there was never any music that was cheaper than bluegrass. Here’s Jimmie Rodgers, out of Mississippi, laying down “Blue Yodel #9.” By this point, everyone with a radio has heard how to fingerpick a guitar.
Now before the 1940s, the banjo was generally strummed. You could stroke the strings with the backs of your nails, and pick out a melody with your thumb, much like Mother Maybelle did on the guitar above. That playing method was called frailing, and it was “the way a banjo sounded” for decades.
Until The Grand Ole Opry, broadcast out of Nashville since 1927, discovered Lester Flatt and Earl Scruggs in the 1940s. These important early radio broadcasts, seeded the signature metal fingerpick sound, that you probably already associate with banjos.
https://www.youtube.com/watch?v=FtMdqh3HFBo
Technical precision was always a key part of the bluegrass sound. Flatt and Scruggs proved that you didn’t have to play perfectly, as long as you played fast and loud. But at the same time, important bluegrass guitarists like Chet Atkins paved the way for diamond-cutter exactitude from guitarists like Don Felder and Mark Knopfler and Brian May. Rock and roll was popping when Atkins recorded this stately piece in 1954:
Bluegrass took its storytelling roots from Scotch-Irish tradition. And one of the most fascinating vestiges of that tradition, is the murder ballad. The basic idea, is that you’re singing a cloyingly sweet song, about the fact that you beat your girlfriend with a stick and drowned her, for some inadequately explained reason. Murder ballads are weird and spooky as hell, but they come from a long and honorable line of storytelling. Before the Knoxville Girl was the Knoxville Girl, she was the Wexford girl, from Irish ballads of the 1800s; and before she was the Wexford girl, she was the victim in a popular broadside that Samuel Pepys wrote about in his diary. Like I said earlier, I lied when I told you when bluegrass got started. Here’s the Louvin Brothers, from 1954; but really, the story is from 1683 or thereabouts.
So there was never any particular Knoxville girl or boy, but there was Cas Walker of Knoxville, and he was just as bad or worse than any murderer. The Cas Walker Farm and Home Show was a popular variety show broadcast out of Knoxville, from 1929 on, hosted by this particular owner of a chain of local supermarkets. Cas Walker was a legendarily ornery son of a bitch, and is probably worth several books in and of himself:
Anyway, the Knoxville locals that managed to get on the program, got play across Tennessee. A few of those locals managed to make some good of themselves:
Bluegrass music never tolerated the weak. If anything, the bluegrass women were meaner than the men. Here’s Loretta Lynn in 1968, committing interstate transmission of a threatening message:
By 1970, both country music and bluegrass were more or less in final form. Here’s Cherryholmes playing a crossover hit from 2005. There’s nothing in this song that wasn’t in the genre forty years earlier:
From 1970 onward, technical production ability began to trump creative performance ability in country and rock music. The Phil Spector wall-of-sound production technique made popular rock and country into Wagnerian-sized orchestral fireworks.
That’s the opposite of the bluegrass I remember. I choose to give you bluegrass, for the same reason that I would prefer to make you a meal with my own hands. Bluegrass is human. Bluegrass doesn’t come out of machines or recording studios. It comes out of amateur musicians with cheap, out-of-tune voices and cheap, out of tune instruments. It comes out of driveways and trailers and little white churches in the valley. Bluegrass has never, ever been formal. When musicians play the good stuff, the real stuff, they tear instruments apart. Like all things from the heart, bluegrass is full of disorder and complexity and passion and immediacy and love.